Dropout 原理及实现
Dropout 要解决的问题
过拟合: 神经网络中参数量非常大, 很容易导致过拟合.
Dropout 原理oi
dropout 其实就是随机丢弃一些神经元, 从而使得训练的网络并不相同, 起到同时训练多个网络的效果, 如下图所示:
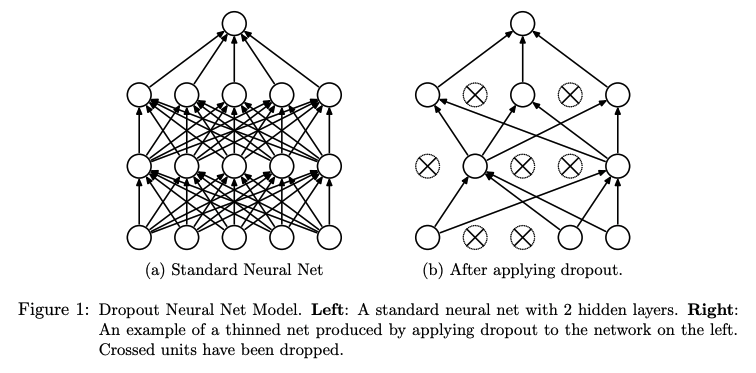
抄两个公式:
1.没有 dropout 的网络为:
\[\begin{gather} z^{(l+1)}_i =& W^{(l+1)}_i y^l + b^{(l+1)}_i \\ y^{(l+1)}_i =& f(z^{(l+1)}_i) \end{gather}\]2.有 dropout 的网络为:
\[\begin{gather} r^{(l)}_j =& Bernoulli(p) \\ \hat {y}^{(l)} =& r^{(l)} * y^{(l)} \\ z^{(l+1)}_i =& W^{(l+1)}_i \hat{y}^{(l)} + b^{(l+1)}_i \\ y^{(l+1)}_i =& f(z^{(l+1)}_i) \end{gather}\]可知, dropout 是根据丢弃概率 p 生成一个伯努利分布, 即 0,1 序列, 作用在 y 上后就能随机隐藏神经元.
因此在测试阶段要同样考虑(乘以)概率 p, 即测试阶段的公式为: \(w^{(l)}_{test} = p W^{(l)}\)
实际上, 为了简化测试阶段的逻辑, 通常是在训练阶段除以 $1-p$, 而测试阶段不作任何改动实现的.
Dropout 优缺点
优点
- 缓解过拟合问题, 类似于多个网络取平均的思想
- 减少神经元之间的共适应关系, 避免某些神经元组合在特定特征下才起作用
缺点
1.训练时间明显增加
Dropout 实现
参考讲解视频, 实现的时候要注意: 保证训练和测试两个阶段的期望相同.
测试阶段需要考虑 p 的实现:
import numpy as np
def train(rate, x, w1, b1, w2, b2):
layer1 = w1 * x + b1
layer1 = np.random.binomial(1, rate, x.shape) * layer1
layer1 = np.maximun(0, layer1)
layer2 = w2 * x + b2
layer2 = np.random.binomial(1, rate, layer1.shape) * layer1
layer2 = np.maximun(0, layer2)
return layer2
def test(rate, x, w1, b1, w2, b2):
layer1 = w1 * x + b1
layer1 = layer1 * (1 - rate)
layer1 = np.maximun(0, layer1)
layer2 = w2 * x + b2
layer2 = layer2 * (1 - rate)
layer2 = np.maximun(0, layer2)
return layer2
测试阶段不考虑 p 的实现:
import numpy as np
def train(rate, x, w1, b1, w2, b2):
layer1 = w1 * x + b1
layer1 = np.random.binomial(1, rate, x.shape) * layer1
layer1 = layer1 / (1 - rate)
layer1 = np.maximun(0, layer1)
layer2 = w2 * x + b2
layer2 = np.random.binomial(1, rate, layer1.shape) * layer1
layer2 = layer2 / (1 - rate)
layer2 = np.maximun(0, layer2)
return layer2
def test(x, w1, b1, w2, b2):
layer1 = w1 * x + b1
layer1 = np.maximun(0, layer1)
layer2 = w2 * x + b2
layer2 = np.maximun(0, layer2)
return layer2
参考链接
[1] Dropout
[2] Dropout 讲解视频